Espacios Vectoriales

¿Qué son los espacios vectoriales?

Un espacio vectorial es una estructura algebraica creada a partir de un conjunto no vacío, una operación interna (llamada suma, definida para los elementos del conjunto) y una operación externa (llamada producto por un escalar, definida entre dicho conjunto y otro conjunto, con estructura de cuerpo), con 8 propiedades fundamentales.

A los elementos de un espacio vectorial se les llama vectores y a los elementos del cuerpo, escalares.

Representación gráfica de un espacio vectorial

Enumere los 8 axiomas para comprobar si un conjunto es un espacio vectorial.

Un espacio vectorial real V es un conjunto de objetos llamados vectores, junto con dos operaciones llamadas suma y multiplicación por un escalar que satisfacen los siguientes axiomas:

Ley de composición interna: si Ū y ṽ son vectores de V, entonces (Ū+ ṽ) está en V.

Propiedad conmutativa: si Ū y ṽ son vectores de V, entonces Ū+ ṽ = ṽ + Ū.

Propiedad asociativa: si Ū, ṽ y ŵ son vectores de V, entonces Ū + (ṽ + ŵ) = (Ū + ṽ) + ŵ.

Existencia del elemento neutro: existe un vector V, denominado vector nulo, tal que para cualquier vector Ū de V: Ō + Ū = Ū+ Ō= Ū.

Existencia del elemento inverso aditivo: para todo vector Ū de V existe un vector – Ū en V, denominado opuesto de Ū tal que Ū+(Ū) = (-Ū) + Ū = Ō.

Ley de composición externa: si A: es cualquier número real y Ū es cualquier vector de V, entonces (A. Ū) está en V.

Propiedad distributiva del producto de un escalar por un vector con respecto a la suma de vector: si A: es cualquier número real y Ū y ṽ son vectores de V, entonces A*(Ū+ ṽ) =A* Ū+A* ṽ.

Propiedad distributiva del producto de un escalar por un vector con respecto a la suma de escalares: si A y B son cualquier par de escalares y Ū es cualquier vector de V entonces (A+B) * Ū=A* Ū+B* Ū.

Asociatividad mixta: si A y B son cualquier par de escalares y Ū es cualquier vector de V entonces A*(B* Ū) = (A*B) * Ū=B*(A* Ū).

Identidad: si Ū es cualquier vector de V, entonces 1* Ū= Ū.

¿Qué es un subespacio vectorial?

Un subespacio vectorial es el subconjunto de un espacio vectorial, que debe cumplir ciertas características específicas.

Sean V y S dos espacios vectoriales definidos en el campo K, entonces S es un subespacio vectorial de V, si y solo si, S ⊆ V. De hecho, todos los espacios vectoriales tienen subconjuntos que también son espacios vectoriales.

Representación gráfica de un subespacio:

Ejemplo:

Enumere las tres propiedades que permiten probar si un subconjunto de un espacio vectorial e u subespacio.

Condición de existencia de subespacio. El criterio para la verificación de que S sea subespacio de V, es que ambas operaciones (+ entre elementos del conjunto S y * con escalares del cuerpo K) sean cerradas, es decir, den como resultado elementos que también pertenezcan a S. 

Para ello se definen 4 axiomas que, de cumplirse, garantizan la existencia del subespacio vectorial. Sea V un espacio vectorial, se define S como subespacio vectorial si y solo si:

1.    S no es un conjunto vacío.

2.    S es igual o está incluido en V.

3.    La suma es ley de composición interna.

4.    El producto es ley de composición externa.

Si estos cuatro axiomas se cumplen entonces el conjunto es un subespacio.

Ejemplo subespacio:

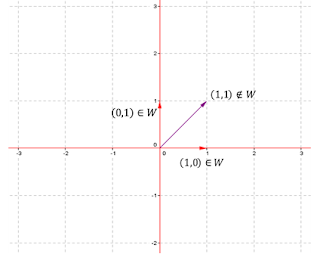
Consideremos el conjunto W={(x,y)∈R2|xy=0}W={(x,y)∈R2|xy=0}, ¿Es un subespacio de R2R2?

Se cumple (a) pues (0,0) ∈W (0,0) ∈W

No se cumple (b) porque la suma de dos vectores de WW puede no estar en WW, por ejemplo:

(1,0) +(0,1) = (1,1) ∉W (1,0) +(0,1) = (1,1) ∉W

Entonces WW no es un subespacio de R2R2.

Explique cuáles son la dimensión y el rango de un subespacio y que es una base.

Dimensión

Rango