Informe solución sistemas de ecuaciones mediante método Gauss

TIA: Informe solución sistemas de ecuaciones mediante método Gauss

Tutor(a)

RUTH BEATRIZ MORENO ECHAVARRIA

Nombres completos:

Franco Anel Ubalde Arenas

23/04/2020

MEDELLÍN

PLANTEAMIENTO DEL PROBLEMA


Primer Punto:

Plantear el sistema de ecuaciones para hallar un número de tres cifras sabiendo que la suma de sus cifras es 11, que la suma de la primera y la tercera cifra es 5 y que la segunda cifra es el doble de la tercera.


RESPUESTA:

X + Y + Z = 11
X + Z = 5
Y = 2Z

Segundo Punto:

Resolver el siguiente sistema de ecuaciones por el método de Gauss
x + 2y - 3z = -16
3x + y - 2z = -10
2x - 3y + z = -4

RESPUESTA:

La matriz


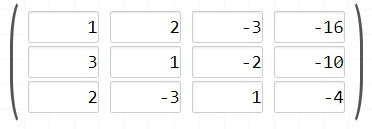
Encuentra el pivote en la columna número 1 en la fila número 1


Multiplica la fila número 1 por 3


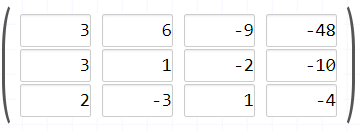
Sustrae la fila número 1 de la fila número 2 y restaurarla


Multiplica la fila número 1 por 2


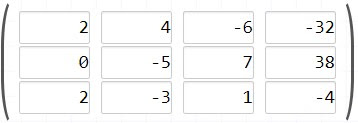
Sustrae la fila número 1 de la fila número 3 y restaurarla


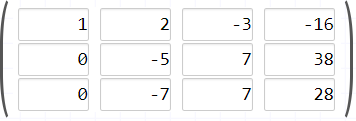
Encuentra el pivote en la columna número 2 dividiendo la fila número 2 entre -5


Multiplica la fila número 2 por 2


Sustrae la fila número 2 de la fila número 1 y restaurarla


Multiplica la fila número 2 por -7


Sustrae la fila número 2 de la fila número 3 y restaurarla


Encuentra el pivote en la columna número 3 dividiendo la fila número 3 entre -14/5



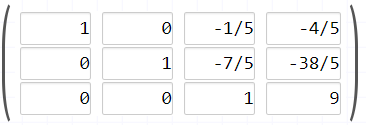
Multiplica la fila número 3 por -1/5


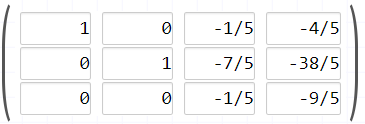
Sustrae la fila número 3 de la fila número 1 y restaurarla


Multiplica la fila número 3 por -7/5


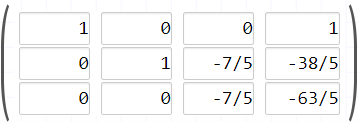
Sustrae la fila número 3 de la fila número 2 y restaurarla


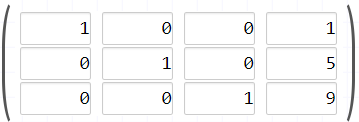
SOLUCIÓN:

X= 1
Y= 5
Z= 9

Tercer Punto:

Resolver el siguiente sistema de ecuaciones lineales x + y + z = 3
2x + 4y - 5z = 21
2y + 3z = 15

RESPUESTA:

La matriz


Encuentra el pivote en la columna número 1 en la fila número 1


Multiplica la fila número 1 por 2


Sustrae la fila número 1 de la fila número 2 y restaurarla


Encuentra el pivote en la columna número 2 dividiendo la fila número 2 entre 2


Resta la fila número 2 por la fila número 1


Multiplica la fila número 2 por 2


Sustrae la fila número 2 de la fila número 3 y restaurarla


Encuentra el pivote en la columna número 3 dividiendo la fila número 3 entre 10

Multiplica la fila número 3 por 9/2


Sustrae la fila número 3 de la fila número 1 y restaurarla


Multiplica la fila número 3 por -7/2


Sustrae la fila número 3 de la fila número 2 y restaurarla


SOLUCIÓN:

X= -9/2
Y= 15/2
Z= 0

¡Muy importante! Para tener en cuenta:

Muestre la matriz ampliada original de cada sistema de ecuaciones en cada uno de los puntos.
Indique las operaciones elementales y cada matriz resultante después aplicar cada paso.
En cada punto debe hacer una reflexión si el sistema tiene solución, si es única y en caso de no tenerla, por qué no la tiene.
Si requiere de más espacio para el desarrollo puede agregar páginas necesarias.