create database Arrendamientos
use Arrendamientos
--CREAR TABLAS
--Creacion de tabla Sede
Create Table Sede(
codigo int,
codigo_administracion int,
nombre_administracion varchar(30),
constraint pk_cs primary key(codigo)
)
-- Creacion de tabla Propiedad
Create Table Propiedad(
codigo int,
tipo varchar (30),
direccion varchar (50),
tamaño_metros int,
numero_habitaciones int,
precio bigint,
propietario varchar (50),
fecha_ultimo_arriendo datetime,
fecha_fin_ultimo_arriendo datetime,
Constraint pk_cp primary key(codigo)
)
--Creacion de tabla Fiador
Create Table Fiador(
nombre varchar (30),
cedula_fiador bigint,
codigo_propiedad int,
Constraint pk_nf primary key(cedula_fiador),
Constraint fk_cpf foreign key(codigo_propiedad) references Propiedad(codigo)
)
--Creacion de tabla Cliente
Create Table Cliente(
cedula bigint,
nombre varchar (50),
certificado_laboral varchar (30),
cedula_fiador bigint,
Constraint pk_cc primary key(cedula),
Constraint fk_nf1 foreign key(cedula_fiador) references Fiador(cedula_fiador)
)
--Creacion de tabla Contrato
Create Table Contrato(
codigo int,
codigo_propiedad int,
cedula_cliente bigint,
precio bigint,
fecha_inicio datetime,
duracion_meses int,
Constraint pk_cCo primary key(codigo),
Constraint fk_cp1 foreign key(codigo_propiedad) references Propiedad(codigo),
Constraint fk_cc1 foreign key(cedula_cliente) references Cliente(cedula)
)
--Creacion de tabla Pago
Create Table Pago(
codigo int,
codigo_contrato int,
cedula_cliente bigint,
fecha_pago datetime,
valor bigint,
Constraint pk_cp2 primary key(codigo),
Constraint fk_cCo1 foreign key(codigo_contrato) references Contrato(codigo),
Constraint fk_cc2 foreign key(cedula_cliente) references Cliente(cedula),
)
lunes, 27 de abril de 2020
jueves, 23 de abril de 2020
Informe solución sistemas de ecuaciones mediante método Gauss
TIA: Informe solución sistemas de ecuaciones mediante método Gauss
Tutor(a)
RUTH BEATRIZ MORENO ECHAVARRIA
Nombres completos:
Franco Anel Ubalde Arenas
23/04/2020
MEDELLÍN
PLANTEAMIENTO DEL PROBLEMA
Primer Punto:
Plantear el sistema de ecuaciones para hallar un número de tres cifras sabiendo que la suma de sus cifras es 11, que la suma de la primera y la tercera cifra es 5 y que la segunda cifra es el doble de la tercera.
RESPUESTA:
X + Y + Z = 11
X + Z = 5
Y = 2Z
Primer Punto:
Plantear el sistema de ecuaciones para hallar un número de tres cifras sabiendo que la suma de sus cifras es 11, que la suma de la primera y la tercera cifra es 5 y que la segunda cifra es el doble de la tercera.
RESPUESTA:
X + Y + Z = 11
X + Z = 5
Y = 2Z
Resolver el siguiente sistema de ecuaciones por el método de Gauss
x + 2y - 3z = -16
3x + y - 2z = -10
2x - 3y + z = -4
La matriz
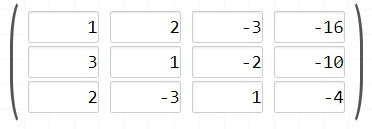
Encuentra el pivote en la columna número 1 en la fila número 1

Multiplica la fila número 1 por 3
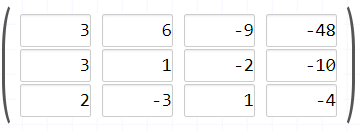
Sustrae la fila número 1 de la fila número 2 y restaurarla

Multiplica la fila número 1 por 2
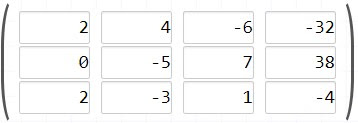
Sustrae la fila número 1 de la fila número 3 y restaurarla
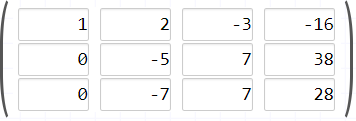
Encuentra el pivote en la columna número 2 dividiendo la fila número 2 entre -5

Multiplica la fila número 2 por 2

Sustrae la fila número 2 de la fila número 1 y restaurarla

Multiplica la fila número 2 por -7

Sustrae la fila número 2 de la fila número 3 y restaurarla

Encuentra el pivote en la columna número 3 dividiendo la fila número 3 entre -14/5
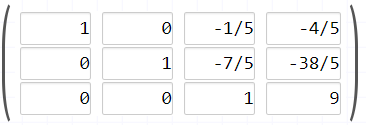
Multiplica la fila número 3 por -1/5
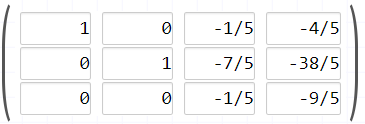
Sustrae la fila número 3 de la fila número 1 y restaurarla

Multiplica la fila número 3 por -7/5
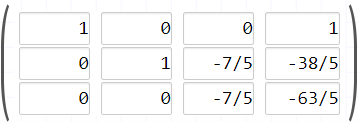
Sustrae la fila número 3 de la fila número 2 y restaurarla
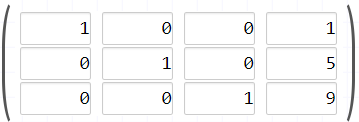
SOLUCIÓN:
X= 1
Y= 5
Z= 9
Resolver el siguiente sistema de ecuaciones lineales x + y + z = 3
2x + 4y - 5z = 21
2y + 3z = 15
RESPUESTA:
La matriz

Encuentra el pivote en la columna número 1 en la fila número 1

Multiplica la fila número 1 por 2

Sustrae la fila número 1 de la fila número 2 y restaurarla

Encuentra el pivote en la columna número 2 dividiendo la fila número 2 entre 2

Resta la fila número 2 por la fila número 1

Multiplica la fila número 2 por 2

Sustrae la fila número 2 de la fila número 3 y restaurarla

Encuentra el pivote en la columna número 3 dividiendo la fila número 3 entre 10

La matriz

Encuentra el pivote en la columna número 1 en la fila número 1

Multiplica la fila número 1 por 2

Sustrae la fila número 1 de la fila número 2 y restaurarla

Encuentra el pivote en la columna número 2 dividiendo la fila número 2 entre 2

Resta la fila número 2 por la fila número 1

Multiplica la fila número 2 por 2

Sustrae la fila número 2 de la fila número 3 y restaurarla

Encuentra el pivote en la columna número 3 dividiendo la fila número 3 entre 10

Muestre la matriz ampliada original de cada sistema de ecuaciones en cada uno de los puntos.
Indique las operaciones elementales y cada matriz resultante después aplicar cada paso.
En cada punto debe hacer una reflexión si el sistema tiene solución, si es única y en caso de no tenerla, por qué no la tiene.
Si requiere de más espacio para el desarrollo puede agregar páginas necesarias.
miércoles, 1 de abril de 2020
Matrices Especiales
Matriz simétrica: una matriz cuadrada es simétrica cuando los elementos a ambos lados de la diagonal principal son iguales. aij = aji
Matriz identidad: matriz cuadrada donde los elementos de la diagonal principal son unos y el resto ceros. Se representa por I2 la matriz identidad de orden 2, I3 la identidad de orden 3, I4 la de orden 4, etc.
Matriz triangular inferior: todos los elementos por encima de la diagonal principal son cero.
Matriz diagonal: matriz cuadrada donde los elementos que no están en la diagonal principal son cero.
- Bidiagonal superior: es una matriz cuyos elementos por encima de la diagonal 1 y debajo de la diagonal principal son 0.
- Bidiagonal inferior: es una matriz cuyos elementos por debajo de la diagonal -1 y encima de la diagonal principal son 0.
- Tridiagonal: es una matriz cuyos elementos por encima de la diagonal 1 y debajo de la diagonal -1 son 0.
- Por filas cuando, para todas las filas, el valor absoluto del elemento de la diagonal de esa fila es estrictamente mayor que el resto de elementos de esa fila.
- Por columnas cuando, para todas las columnas, el valor absoluto del elemento de la diagonal de esa columna es estrictamente mayor que el resto de elementos de esa columna.
Matriz traspuesta: La matriz traspuesta de una matriz A se denota por AT y se obtiene cambiando sus filas por columnas (o viceversa).
Matriz adjunta o de cofactores: es una matriz obtenida a partir de otra, que traspuesta y dividida por el determinante de esta otra es igual a la matriz inversa de la matriz de partida. En otras palabras, es aquella en la que cada elemento se sustituye por su adjunto.
Matriz de Hessenberg superior: es una matriz cuadrada de dimensión n>1 cuyos elementos por debajo de la diagonal -1 son 0.
Matriz de Hessenberg inferior: es una matriz cuadrada de dimensión n>1 cuyos elementos por encima de la diagonal 1 son 0.
Suscribirse a:
Comentarios (Atom)
Reconociendo lo Aprendido UD1 - IoT
El Internet de las cosas (IoT) es el proceso que permite conectar elementos físicos cotidianos al Internet: desde objetos domésticos comunes...

-
Modelo “4+1” vistas de Kruchten El modelo “4+1” de Kruchten, es un modelo de vistas [1] diseñado por el profesor Philippe Kruchten y que...
-
Las bases de datos son el pilar de la vida del ser humano actual. A continuación una pequeña reseña de las bases de datos, alli no termina...
-
Antecedentes de la metodología de la investigación para el desarrollo del conocimiento. Las explicaciones del mundo y de los fenómenos se pu...





















